An Introduction
- fiebm8842
- Oct 30, 2023
- 2 min read
Updated: Dec 7, 2023
10/30/23
My name is Morgan Fiebig and I am a junior at the University of Wisconsin- Eau Claire. My major is in mathematics with a research emphasis and a minor in computer science. I was accepted into the Ronald E. McNair Scholars program last spring and joined this fall in the 2025 cohort. This blog is intended to document my journey through the McNair program as I work towards my academic and career goals of obtaining a PhD in mathematics and pursuing a career in academia.
My Research Experiences
When I first arrived in Eau Claire in the fall of 2022, I was returning to college after a four year pause in my education. I knew that it was going to be a challenge for me to pick up right where I left off those few years ago. During the first week of classes, my data science professor Dr. Sylviana Amethyst sent out an email to the mathematics department to announce she was looking for a student researcher. This was surprising to me- in my experience at other institutions, it can be quite difficult to come upon such an opportunity. I joined her project in the fall of 2022, and we will continue to work together this year. The overarching goal of our project is improving bertini_real to make 3D printable algebraic surfaces which preserve as much of the mathematical authenticity of the surface as possible. This year, our focus is mainly on improving the triangulation of surface meshing and solving other problems such as optimal edge merging and face merging in n-dimensions.
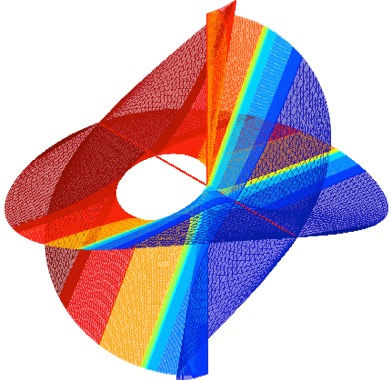
This is an image of Solitude, an algebraic surface that originates from Herwig Hauser's Algebraic Surface's Gallery. The points and curves which determine the rendering of this surface were computed with Bertini_real.
Over the summer I began working with Dr. aBa Mbirika (he goes by aBa) in his projects involving second order linear recurrence sequences modulo m. We say that a number a is congruent to b modulo m if b is the remainder upon dividing a by m. Our aim is to generalize some well known results of the famous Fibonacci sequence to several other sequences. In particular, we have been exploring patterns in the entry points and Pisano periods. An entry point is the first occurrence of zero when taking the sequence modulo m, or, in other words, the first sequence term which is congruent to zero modulo m. The Pisano period is the length of the fundamental period, which is the block of terms that repeat infinitely to make up the entire sequence. As of now, some of our largest results are pertaining to the Pell, associated Pell, balancing, and Lucas-balancing sequences. In January 2024 I will be presenting our research at the Joint Mathematics Meeting in San Francisco. You can find the abstract for my talk here.
For me, this is just the beginning. My mathematical interests continue to grow each day and I am truly excited to see where the rest of my time as a McNair scholar will take me.

Comments